On algebraic differentiators
Algebraic differentiators have been derived and discussed in the systems and control theory community. The initial works based on differential-algebraic methods have been developed by Mboup, Join, and Fliess in [2]. These numerical, non-asymptotic approximation approaches for higher-order derivatives of noisy signals are well suited for real-time embedded systems. A historical overview and a detailed discussion of these differentiators and their time-domain and frequency-domain properties are given in the survey [1].
The approximation-theoretic derivation recalled in the survey [1] permits the interpretation of the estimation process by the following three steps illustrated in the figure below stemming from [1]:
Projection: At time \(t\), the sough \(n\)-th order time derivative \(y^{(n)}\) over the interval \(I_T(t)\) is projected onto the space of polynomials of degree \(N\). This yields the polynomial \(p_N\) depicted in the left and middle part of Figure 2.
Evaluation: The polynomial \(p_N\) is evaluated at \(t-\delta_t\), which gives an estimate \(\hat{y}^{(n)}(t)=p_N(t-\delta_t)\) for the derivative \(y^{(n)}\) as depicted in the central part of Figure 2. Choosing the delay to be the largest root of a special Jacobi polynomial increases the approximation order by 1 with a minimal delay. Alternatively, a delay-free estimation or even a prediction of the future derivative might be selected, at the cost of a reduced accuracy.
Repetition: The first two steps are repeated at each discrete time instant while keeping the parameters of the differentiator constant. This yields the estimate \(\hat{y}^{(n)}\) depicted in the right part of the Figure 2.

Figure 2. Three-step process of the estimation of the \(n\)-th order derivative \(y^{(n)}\mapsto y^{(n)}(t)\) of a signal \(y\mapsto y(t)\) using algebraic differentiators (figure from [1])
Algebraic differentiators can be interpreted as linear time-invariant filters with a finite-duration impulse response. Figure 3 visualizes the online estimation process of the first derivative of a noisy signal. The filter window, the buffered signal, and the filter kernel can be clearly seen.
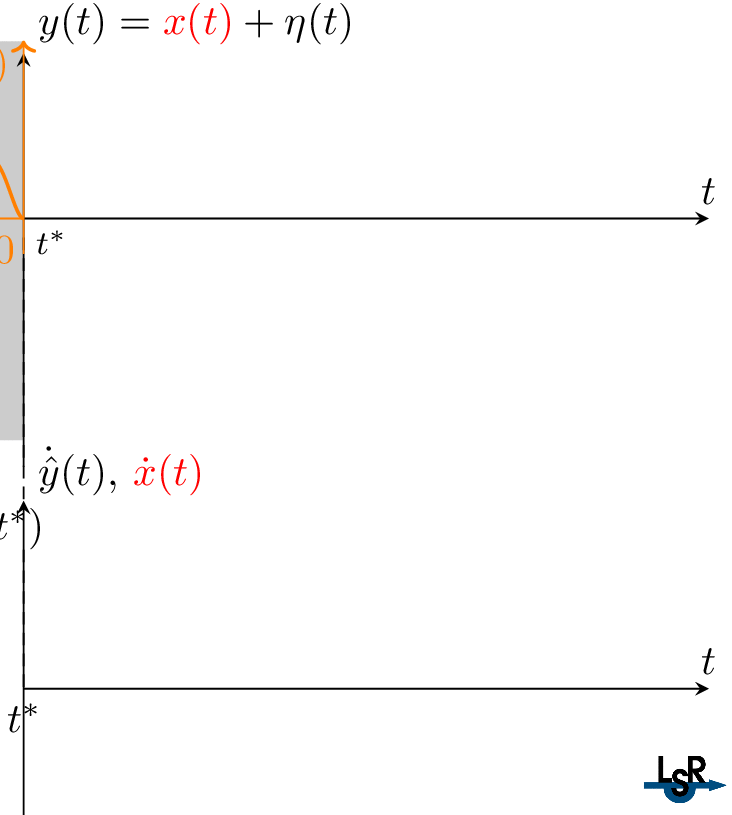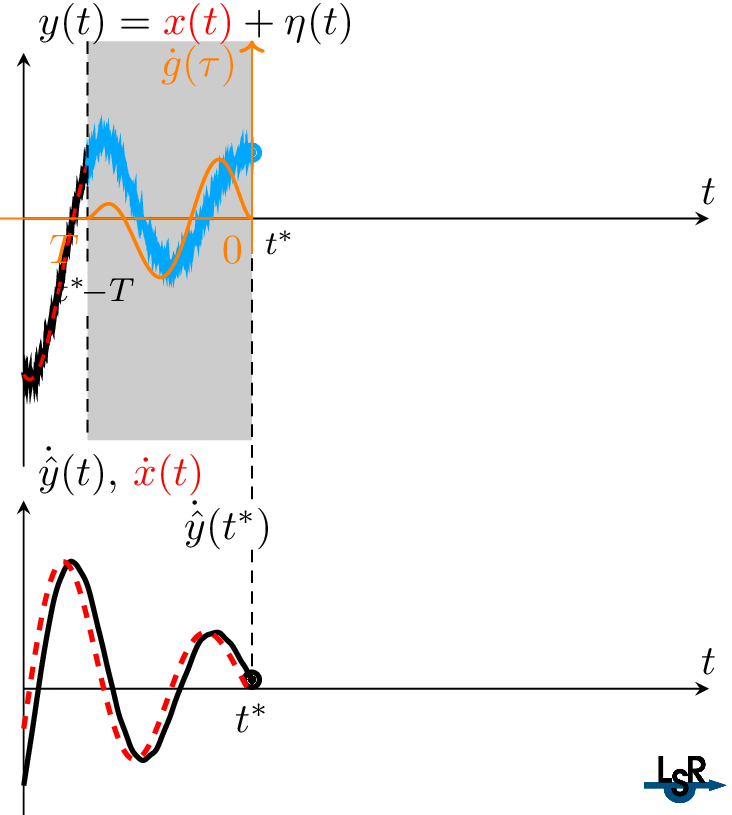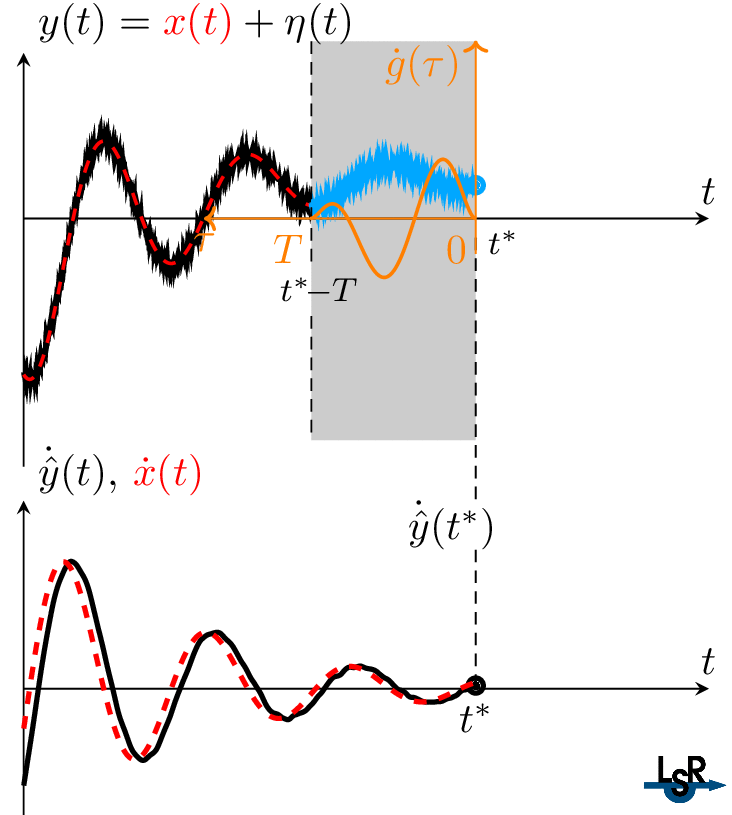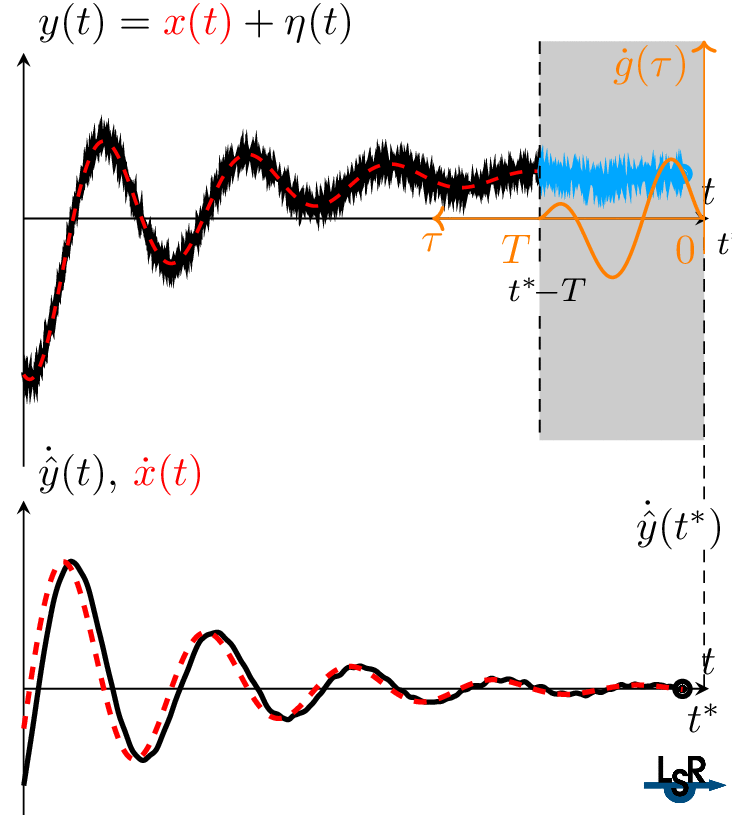
Figure 3. Visualization of the online estimation of the first derivative a noisy signal using an algebraic differentiator.
These filters can be approximated as lowpass filters with a known cutoff frequency and a stopband slope. Figure 4 presents the amplitude and phase spectra of two exemplary filters. The lowpass approximation is also shown.

Figure 4. Amplitude and phase spectra of two different filters and the corresponding lowpass approximation of the amplitude spectrum.
See [1], [3], [4], and [5] for more details on the parametrization of these differentiators.